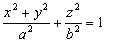Strumenti Utente
Barra laterale
Indice
Geodesia
La Geodesia è la scienza che si occupa dello studio della forma e delle dimensioni della superficie di riferimento terrestre, del suo campo gravitazionale e dei fenomeni geodinamici quali per e sempio lo spostamento dei poli, le maree terrestri e i movimenti della crosta(Geodesia teorica). La Geodesia si occupa anche della elaborazione di teorie e procedimenti operativi finalizzati alla conoscenza, la descrizione, la misura e la rappresentazione di zone più o meno estese della Terra (Geodesia operativa).
La scienza che studia gli strumenti ed i metodi operativi, di calcolo e di disegno, necessari alla rappresentazione grafica, di una parte più o meno estesa della superficie terrestre è invece la topografia (dal greco topos, luogo e graphein, scrivere).
Uno degli apetti più importanti della cartografia è quello di dare una rappresentazione di tutta la superficie del territorio da rappresentare in un sistema di riferimento unico e condiviso. Il territorio è pertanto rappresentato sia dal punto di vista altimetrico che da quello planimetrico. La rappresentazione altimetrica si ottiene attribuendo una quota ad ogni generico punto della superficie fisica della Terra; tale quota è data dalla distanza, lungo la verticale passante per il punto, da una superficie di riferimento detta geoide. La rappresentazione planimetrica, viene fatta mettendo in relazione i punti della superficie terrestre con i punti del sistema cartesiano piano, detto proiezione cartografica, tramite una superficie matematica intermedia di passaggio rappresentata dall’ellissoide di riferimento.
La terra, il geoide e l'ellissoide
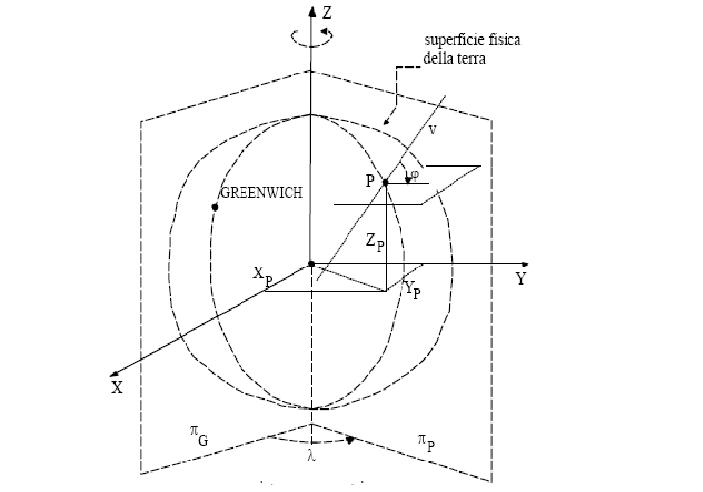
Uno dei primi problemi che i geodeti si trovarono ad affrontare fu quello di definire una superficie matematica della Terra che permettesse di mettere in corrispondenza i punti della superficie fisica della Terra con i punti di un sistema cartesiano piano. Per fare ciò, venne scelta una terna cartesiana ortogonale (X, Y, Z) che potesse rappresentare un sistema di riferimento rispetto al quale riferire le coordinate della superficie matematica (Fig.1).
Fig.1 Sistema geocentrico e coordinate geografiche terrestri (Galleto, Spalla 1999).
Tale terna può essere definita come segue:
• origine della terna nel baricentro della massa terrestre;
• asse Z coincidente con l’asse di rotazione terrestre;
• asse X ortogonale a Z nel baricentro della massa terrestre nel piano contenente il punto di intersezione tra il meridiano di Greenwich e l’equatore.
Tale sistema prende il nome di sistema geocentrico.
Dato un punto P sulla superficie fisica della Terra, si definisce piano del meridiano terrestre passante per P il piano contenente l’asse di rotazione terrestre ed il punto P.
Ogni punto P della superficie della Terra è individuabile in due diversi modi:
• in funzione delle sue coordinate X, Y, Z nel sistema geocentrico;
• in funzione di una coppia di coordinate geografiche terrestri rappresentate dalla latitudine terrestre e dalla longitudine terrestre.
La latitudine terrestre è l’angolo che la verticale passante per il punto P forma con un generico piano ortogonale all’asse di rotazione terrestre, in particolare con il piano equatoriale; la longitudine terrestre è, invece, l’angolo diedro che il piano, contenente il punto P e l’asse di rotazione terrestre, forma con un piano di riferimento della longitudine, che è quello definito dall’asse di rotazione terrestre e dal piano contenente l’asse X, ovvero il piano meridiano passante per Greenwich (Galletto, Spalla, 1999).
Per definire l’espressione matematica della Terra, i geodeti presero come dato di partenza il suo campo gravitazionale, partendo dal presupposto che in ogni punto della Terra esiste la forza di gravità, data dalla somma della forza di attrazione Newtoniana e dalla forza centrifuga. Venne assunta, quindi, come superficie matematica della Terra una superficie che è sempre perpendicolare alle linee di forza del campo gravitazionale; ma poiché di queste linee ne esistono infinite, se ne scelse una in particolare, cioè quella passante per il livello medio del mare in un preciso punto della superficie terrestre. Tale superficie è detta geoide.
In modo riduttivo, si può affermare che il geoide è la superficie che si otterrebbe prolungando al di sotto delle terre emerse la superficie del mare in assenza delle perturbazioni accidentali o periodiche (maree, venti, correnti ecc.), (ovvero, di equilibrio idrostatico assunta dalla superficie degli oceani), detta anche superficie del livello medio del mare (misurato dai mareografi).
Un punto qualsiasi dello spazio prima di essere riportato nel piano della carta s’immagina trasferito sul geoide, proiettandolo verticalmente, quindi secondo la verticale del luogo. Tuttavia, la formulazione matematica del geoide risulta assai complessa in relazione al fatto che in essa figurano grandezze non solo geometriche, ma anche meccaniche quali la densità dei diversi punti all'interno della massa della terra. Quindi, si sono definite altre superfici di riferimento che approssimano il geoide, per le quali è possibile individuare espressioni matematiche più semplici.
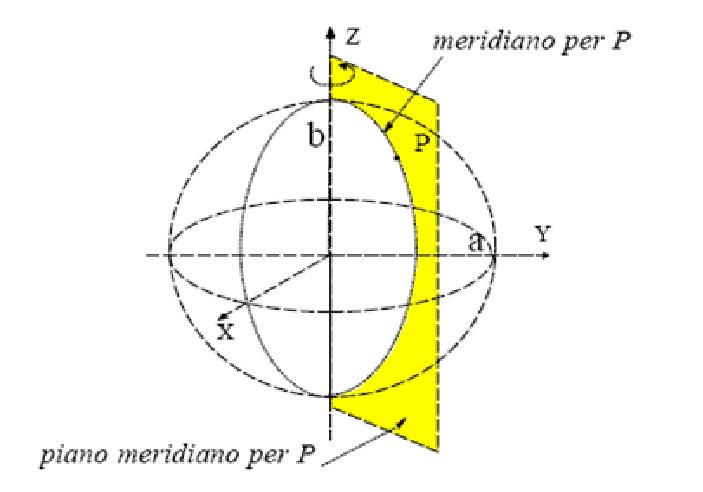
L’ellissoide, che rappresenta la forma matematica più idonea a rappresentare la superficie della Terra, non è altro che la superficie generata dalla rotazione di un’ellisse di semiassi a e b intorno all’asse Z, coincidente con l’asse di rotazione terrestre. Tale ellissoide è detto geocentrico (Fig. 2).
Fig. 2 Ellissoide di rotazione geocentrico (Galletto Spalla 1999).
Dato un punto P sulla superficie dell’ellissoide, si definisce piano meridiano di P il piano contenente l’asse di rotazione Z ed il Punto P; si definisce meridiano di P l’intersezione di detto piano con la superficie dell’ellissoide. L’espressione matematica piuttosto semplice dell’ellissoide permette di mettere agevolmente in corrispondenza i suoi punti con quelli di un sistema di coordinate cartesiane piane. L’espressione
Nella quale a = 6378388,00 m rappresenta il semiasse equatoriale dell'ellissoide e b=6356912,00 m il semiasse polare. I valori di a e di b sopra riportati sono quelli determinati dal geodeta Hayford nel 1909 e tutt’ora utilizzati per definire l’ellissoide internazionale di riferimento. I geodeti delle varie nazioni decisero di adottare non l’ellissoide geocentrico, ma un ellissoide di uguale dimensione e forma di quello geocentrico, ma leggermente ruotato e traslato rispetto ad esso, in modo tale da realizzare la condizione di tangenza al geoide in un punto baricentrico del territorio da rappresentare (Galletto, Spalla,1999). Per l’Italia, i geodeti italiani scelsero alla fine dell’800 di realizzare questa coincidenza tra ellissoide nazionale e geoide in corrispondenza dell’Osservatorio di Monte Mario a Roma (sistema Roma 40) e successivamente in corrispondenza di Postdam in Germania (sistema ED 50).
Sistemi di proiezione cartografica
Le carte geografiche sono delle rappresentazioni sul piano (nella forma di elaborato grafico o informatico) della superficie fisica terrestre ad una scala 1/n assegnata, secondo norme e segni convenzionali prestabiliti. Le proiezioni sono i metodi adottati per riportare e trasformare il reticolato geografico in reticolato piano, allo scopo di ottenere la rappresentazione di una parte o dell’intera superficie terrestre. Quindi, le proiezioni sottendono l’impiego di mezzi geometrici e si possono distinguere in:
• proiezioni prospettiche pure: quando la proiezione avviene su di un piano tangente all’ellissoide in un determinato punto. A seconda della posizione del centro di proiezione, si avranno proiezioni centrografiche, stereografiche, scenografiche, ortografiche, ecc (Fig. 3);
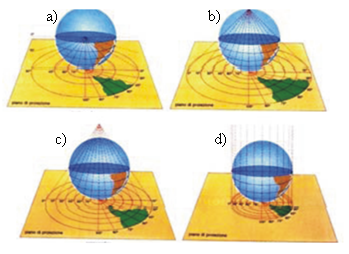
Figura 3: Proiezioni prospettiche: a. centrografica, b. stereografica, c. scenografica, d. ortografica
• proiezioni cilindriche pure: quando la proiezione dei punti dell’ellissoide avviene su una superficie avvolgente (cilindrica o conica), posta tangente all’ellissoide e il centro di proiezione al centro dell’ellissoide o lungo la direzione normale alla linea di tangenza (Fig. 4).
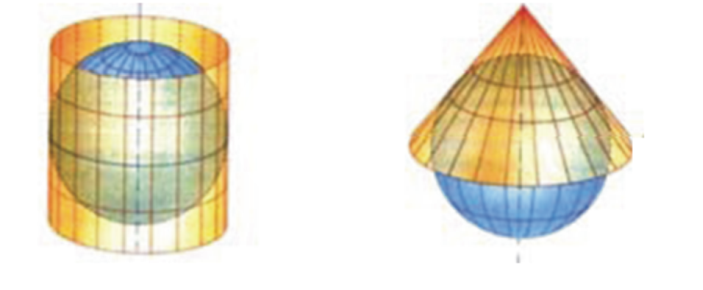
Figura 4: proiezione cilindrica e proiezione conica
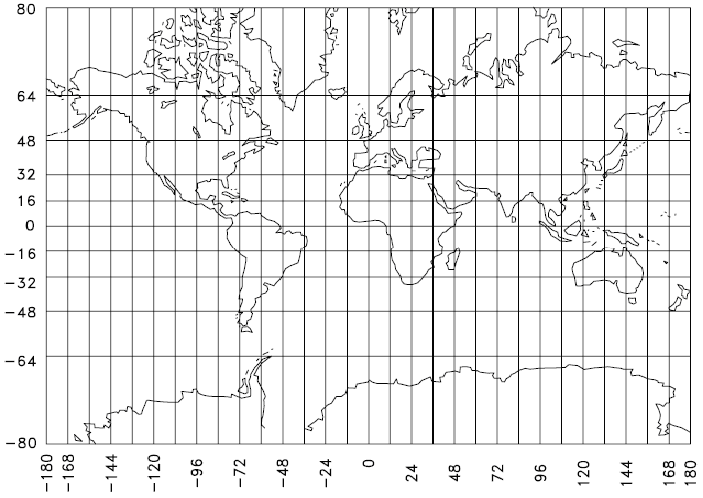
Tra queste ultime, la più nota è la Proiezione cilindrica isogona di Mercatore (Fig. 5). In tale proiezione, meridiani e paralleli sono rettilinei e perpendicolari fra loro; i paralleli invece di avvicinarsi nelle regioni polari, si allontanano, risultando più fitti all’equatore che verso i poli. Quindi, i meridiani rimangono equidistanti, mentre nella realtà si avvicinano gradualmente fra loro verso latitudini crescenti. Di conseguenza, i paralleli si allontanano l’un l’altro nella proporzione di quanto la distanza dei meridiani è maggiorata sulla carta rispetto alla realtà (Pigato, 2000).
Figura 5: Proiezione cilindrica isogona di Mercatore
Rappresentazione di Gauss
Per Carta di Gauss intendiamo un sistema di coordinate cartesiane piane N ed E e due funzioni f e g che mettono in relazione un generico punto P dell'ellissoide, dato attraverso le coordinate geografiche (latitudine e longitudine) φ e λ, e il punto corrispondente P' del sistema cartesiano. La rappresentazione di Gauss è stata scelta per la cartografia ufficiale italiana
Per passare dal sistema ellissoidico, ad un sistema piano N, E sono state ricavate da Gauss delle formule di trasformazione f (φ, λ) e g (φ, λ) imponendo le seguenti condizioni: • l'equatore ellissoidico deve trasformarsi nell'asse delle ascisse E; • il meridiano ellissoidico assunto come origine delle longitudini deve trasformarsi nell'asse delle ordinate N; • un arco di lunghezza m sul meridiano origine deve trasformarsi in un segmento di uguale lunghezza sull'asse delle ordinate N; • l'angolo α formato da due direzioni uscenti da un punto sull'ellissoide deve mantenersi uguale a quello delle corrispondenti direzioni riportate nella carta; • il coefficiente di deformazione, pur variando da punto a punto, deve essere uguale in tutte le direzioni uscenti da un punto. Da queste condizioni analitiche sono state ottenute le due funzioni si f (φ, λ) e g(φ,λ) che applicate alle coordinate, generano una proiezione analoga a quella che si otterrebbe proiettando i punti dell'ellissoide, dal centro dell'ellissoide, su un cilindro tangente all'ellissoide lungo il meridiano origine delle longitudini (Fig. 6) (Galletto, Spalla, 1999).
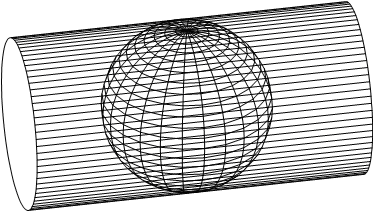
Figura 6: Cilindro tangente a un meridiano
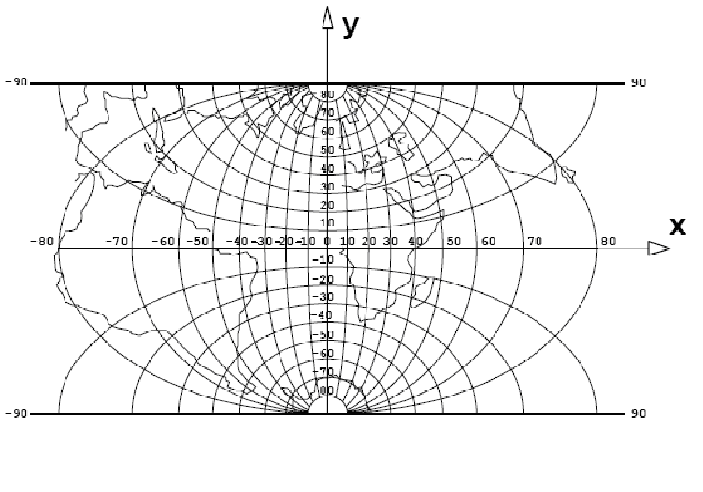
La cartografia di Gauss è conforme, e pertanto gli angoli misurati sulla carta corrispondono perfettamente con i rispettivi angoli misurati sul terreno; le lunghezze misurate sulla carta sono invece leggermente deformate rispetto a quelle misurate sulla superficie di riferimento. Nella figura 7 che segue è riportata una rappresentazione del reticolato geografico, ovvero il complesso di linee che rappresentano le trasformate dei meridiani e dei paralleli: si noti che la trasformata del meridiano centrale è un segmento di retta. Si può facilmente constatare dalla figura 7 come il meridiano centrale venga rappresentato senza subire alcuna deformazione e come invece la deformazione cresca rapidamente allontanandosi dal meridiano centrale.
Figura 7: Proiezione di Gauss
Per limitare le deformazioni, le rappresentazioni cartografiche usualmente utilizzate limitano l'estensione del fuso (porzione di ellissoide compresa tra due meridiani) che viene rappresentato in un unico sistema. La rappresentazione di Gauss viene definita conforme cilindrica inversa, nota anche come proiezione trasversa di Mercatore.
Il sistema U.T.M. (Universal Transverse Mercator)
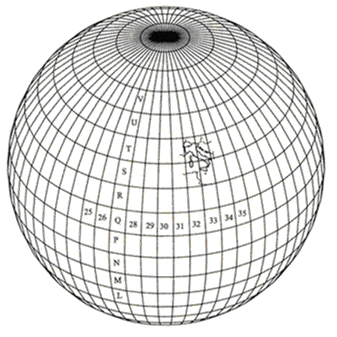
Nel sistema U.T.M., la Terra viene suddivisa in 60 fusi di ampiezza pari a 6° di longitudine, numerati da 1 a 60 procedendo da Ovest verso Est e dando il numero 01 al fuso corrispondente all'antimeridiano di Greenwich (fig. 8). Ogni fuso è stato suddiviso in 20 fasce di ampiezza pari a 8° di latitudine ciascuna, individuate da una lettera maiuscola; ciascuna zona, individuata dall’intersezione di un fuso con una fascia, viene ulteriormente suddivisa in quadrati di 100 Km di lato, con rette parallele agli assi N ed E individuati da due lettere maiuscole. Un punto viene identificato mediante coordinate alfanumeriche (numero del fuso, dalla lettera della fascia, dalla coppia di lettere del quadrato ed infine dalle sue coordinate piane riferite al vertice SO del quadrato di 100 km di lato). A differenza della rappresentazione di Gauss, nella cartografia UTM la coordinata Nord ha origine sull’equatore, mentre, allo scopo di eliminare l'uso dei numeri negativi per le ascisse dei numeri posti ad Ovest dei rispettivi meridiani centrali, si è ricorso allo spostamento fittizio dell'origine delle ascisse, istituendo una falsa origine e attribuendo ai punti sul meridiano centrale di ogni fuso un valore convenzionale dalla coordinata Est pari a 500 km. Si vengono quindi a determinare le coordinate E (Est) e N (Nord), definite da: N = y ; E = 500 ± x (De Toma, 1999)
Figura 8: Fusi di ampiezza 6° previsti dal sistema di UTM
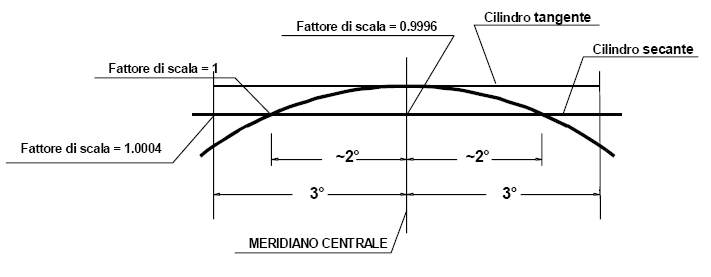
Nell'ambito di un fuso la deformazione lineare raggiunge il valore massimo sui meridiani esterni del fuso: il modulo di deformazione lineare, definito come rapporto tra un elemento lineare infinitesimo sulla carta ed il corrispondente elemento misurato sull'ellissoide, raggiunge il valore di 1.0008, il che significa che considerando due punti ad una distanza di 1000 m sull'ellissoide si trova sulla carta, fra i corrispondenti di tali punti secondo le f e g , una distanza pari a 1000.80 m. Per limitare questa deformazione si introduce un fattore di contrazione pari a 0.9996, ovvero si rimpicciolisce tutta la rappresentazione di 4/10.000. Si ha pertanto un modulo di deformazione lineare di 0.9996 sul meridiano centrale, di 1.0004 sui meridiani estremi e un modulo unitario su due linee prossime ai meridiani che hanno circa 2° di differenza di longitudine rispetto al meridiano centrale: in tale modo la deformazione relativa non supera il valore di 4/10.000, che risulta inferiore all’errore di graficismo commesso nella redazione della carta. Dal punto di vista geometrico, l'applicazione del fattore di contrazione corrisponde ad utilizzare un cilindro non più tangente, bensì leggermente più piccolo, e quindi secante, rispetto all'ellissoide (Fig. 9).
Figura 9: Cilindro tangente e cilindro secante nella rappresentazione di Gauss
ROMA 40: Il sistema Italiano GAUSS-BOAGA
La cartografia ufficiale italiana, proposta nel 1940 dal prof. Boaga, utilizza anch'essa, come il sistema U.T.M., la rappresentazione di Gauss, ma prevede unicamente l'utilizzo di due fusi, denominati fuso Ovest e fuso Est, coincidenti approssimativamente rispettivamente con i fusi 32 e 33 del sistema U.T.M. e aventi rispettivamente i meridiani posti a 9° e a 15° ad Est di Greenwich come meridiani centrali. Come punto di emanazione (luogo geometrico in cui la normale all'ellissoide e la verticale, intesa come linea di forza del campo gravitazionale terrestre, sono coincidenti) per il calcolo delle coordinate geografiche di tutti i vertici della rete geodetica italiana fu assunto il vertice di Roma Monte Mario (sistema Roma 40), al quale in seguito ad accurate osservazioni astronomiche, erano state attribuite le seguenti coordinate geografiche:
φ = 41°55'25“.51 λ = 12°27'08”.40
Come ellissoide è stato scelto l'Ellissoide Internazionale proposto da Hayford orientato a Monte Mario. Fu istituita una doppia falsa origine, una per ciascun fuso, attribuendo ai punti sul meridiano centrale del fuso Ovest un valore convenzionale di x pari a 1500 km, ed a quelli sul meridiano centrale del fuso Est un valore di 2520 km. Si venivano quindi a determinare le coordinate E e N, definite da:
N = y per entrambi i fusi
E = 1500 ± x per il fuso Ovest
E = 2520 ± x per il fuso Est
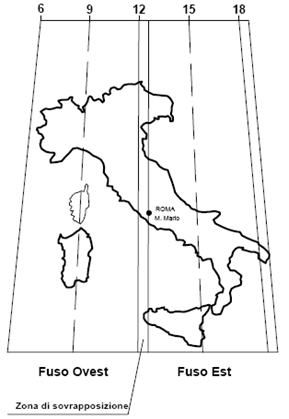
In tal modo la prima cifra della coordinata Est corrisponde sempre al numero del fusoed è quindi pari a 1 per il fuso Ovest e a 2 per il fuso Est. Per collegare le rappresentazioni nei due fusi nazionali è stata creata una zona di sovrapposizione estendendo il fuso Ovest dell'ampiezza di 30' in longitudine; in tale zona i vertici trigonometrici sono riferiti sia al fuso Est sia al fuso Ovest, e sulla cartografia che rappresenta tale zona vengono impressi i riferimenti dei due sistemi. Per consentire poi l'intera rappresentazione del territorio nazionale in soli due fusi, anche il fuso Est è stato esteso di 30' in modo da comprendere la Penisola Salentina che altrimenti sarebbe stata rappresentata su un terzo fuso (Fig. 10).
Figura 10: Suddivisione in fusi per la cartografia ufficiale italiana
In effetti, allo scopo di conservare invariato il taglio della preesistente cartografia in scala 1:25.000 e 1:100.000, la zona di sovrapposizione è stata ottenuta estendendo il fuso Ovest fino al meridiano di Roma (Monte Mario), e quindi il meridiano di separazione tra i due fusi è quello di longitudine 12°27'08“.40 (De Toma, 1999).
ED 50: Il sistema europeo UTM
Negli anni successivi alla Seconda Guerra Mondiale, le nazioni dell’Europa occidentale decisero di unificare le loro reti geodetiche fissando a Postdam, una località in prossimità di Berlino (considerata baricentrica rispetto all’Europa), il punto di emanazione per il calcolo delle coordinate geografiche. In particolare, proprio in tale punto venne imposta la coincidenza tra la normale all'ellissoide e la verticale (normale al geoide). Essendo tale punto diverso da quello adottato dal sistema Roma 40, ci si trova di fronte a degli sfasamenti irregolari tra i due sistemi. Di conseguenza, le coordinate geografiche di Roma Monte Mario hanno subito delle piccole variazioni, risultando di:
φ = 41°55'31”.49 λ = 12°27'10“.93
Questa differenziazione nell’orientamento dell’ellissoide fa sì che uno stesso punto della rete italiana presenta coordinate differenti nei due sistemi, benché si prenda a riferimento la medesima rappresentazione. Questo nuovo sistema identificato con il nome di ED 50 (European Datum, 1950), ha adottato come meridiano fondamentale (0° di longitudine) il meridiano di Greenwich (Fig. 11).
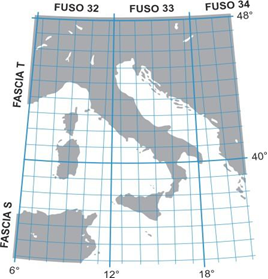
Figura 11: Rappresentazione del Sistema UTM
Analogamente al sistema Roma 40, venne istituita una falsa origine, attribuendo ai punti sul meridiano centrale dei fusi 32 e 33 un valore convenzionale di + 500 Km, in maniera tale da ottenere coordinate sempre positive anche ad ovest del meridiano. Il sistema ED 50 ha inoltre in comune con quello di Roma 40 l’ellissoide di riferimento (ovvero l’ellissoide di Hayford), la proiezione di Gauss con assi cartesiani rappresentati dall’equatore e dai meridiani (Pigato, 2000).
UTM-WGS 84: Il sistema mondiale
Al fine di superare le limitazioni connesse alla possibilità di rappresentare solo parzialmente la superficie fisica della Terra dei precedenti sistemi di riferimento quali il Roma 40 e l’European Datum (ED 50), nel 1984 venne creato un nuovo sistema di riferimento geodetico in grado di coprire tutto il globo terrestre, il World Geodetic System 1984 (WGS84). Si tratta di un sistema globale geocentrico, definito attraverso osservazioni spaziali e costituito da una terna cartesiana destrorsa con origine coincidente con il centro di massa della Terra, l’asse Z diretto verso il polo Nord convenzionale al 1984, l’asse X ortogonale al precedente e intersecante il meridiano di Greenwich al 1984 e l’asse Y diretto in modo da completare una terna destrorsa (Fig.12).
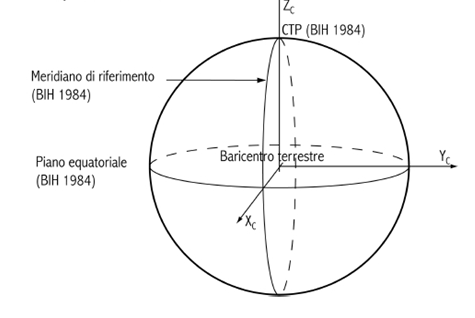
Figura 12: Rappresentazione del sistema WGS 84
A differenza di altri sistemi di riferimento, che si appoggiano all’ellissoide di Hayford, questo nuovo sistema è associato all’ellissoide WGS84, con centro e assi coincidenti con quelli della terna cartesiana.
L’ellissoide WGS84 è definito dai seguenti parametri:
• semiasse maggiore: a = 6378137,00 m;
• schiacciamento: s = 1/298.257223563.
La rappresentazione piana del sistema WGS84 avviene attraverso il sistema cartografico UTM. Il sistema WGS84 rappresenta normalmente il sistema di riferimento per i posizionamenti effettuati con strumenti GPS e la sua realizzazione su scala mondiale è stata curata dal Dipartimento della Difesa degli Stati Uniti. In Europa, la realizzazione del sistema WGS84 è costituita dall’ ETRS89 (EUREF Terrestrial Reference System 1989), mentre in Italia il sistema WGS84 è stato realizzato con l’istituzione della rete geodetica tridimensionale di alta precisione, denominata IGM95, rilevata con strumenti di posizionamento GPS differenziale.
Le coordinate del punto Roma Monte Mario nel sistema WGS84 sono:
• latitudine 41°55’27.851’’;
• longitudine 12°27’07.658’’(da Greenwich).
Link